உகப்பாக்கம் நுட்பங்கள் பொருளாதாரத்தில் முக்கியமானவை, தனிநபர்கள் மற்றும் நிறுவனங்களுக்கு வளங்களை மிகவும் திறமையாகப் பயன்படுத்த உதவுகின்றன. பயன்பாட்டை அதிகரிப்பது, செலவுகளைக் குறைப்பது அல்லது சிக்கலான சிக்கலுக்கு உகந்த தீர்வைக் கண்டறிவது, நியூட்டனின் முறை மற்றும் லாக்ரேஞ்ச் மல்டிபிளையர் முறை போன்ற கணித மேம்படுத்தல் கருவிகள் பொருளாதார பகுப்பாய்வில் சக்திவாய்ந்த கூட்டாளிகள்.
நியூட்டனின் முறை: உகந்த புள்ளிகளைக் கண்டறிதல்
நியூட்டனின் முறை என்ன?
நியூட்டனின் முறை என்பது ஒரு உண்மையான மதிப்புடைய செயல்பாட்டின் வேர்களின் (அல்லது பூஜ்ஜியங்கள்) தோராயங்களைக் கண்டறியப் பயன்படுத்தப்படும் ஒரு மறுசெயல் எண்ணியல் நுட்பமாகும். பொருளாதாரத்தின் பின்னணியில், நியூட்டனின் முறையானது, லாப அதிகரிப்பு, செலவைக் குறைத்தல் அல்லது பயன்பாட்டு மேம்படுத்தல் ஆகியவற்றைக் குறிக்கும் அதிகபட்சம் அல்லது மினிமா போன்ற உள்ளூர் தீவிரத்தை தீர்மானிக்கப் பயன்படுத்தப்படலாம்.
நியூட்டனின் முறைக்கான பொதுவான சூத்திரம்:
\(x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)}\)
இதில்:
- \(x_n\) என்பது தற்போதைய தோராயமாகும்.
- \(f(x_n)\) என்பது \(x_n\) இல் மதிப்பிடப்பட்ட செயல்பாடு ஆகும்.
- \(f'(x_n)\) என்பது \(x_n\) இல் மதிப்பிடப்பட்ட செயல்பாட்டின் வழித்தோன்றலாகும்.
இந்த மறுசெயல் அணுகுமுறையானது தோராய மதிப்பை ஒரு உகந்த மதிப்பு அல்லது ரூட்டாக மாற்றும் வரை அதைச் செம்மைப்படுத்த உதவுகிறது.
பொருளாதாரத்தில் விண்ணப்பம்: செலவு குறைப்பு
ஒரு பொருளின் \(x\) யூனிட்களை உற்பத்தி செய்வதற்கான செலவைக் குறிக்கும் \(C(x)\) செலவுச் செயல்பாட்டைக் கவனியுங்கள். செலவைக் குறைக்கும் உற்பத்தியின் அளவைத் தீர்மானிக்க நியூட்டனின் முறை பயன்படுத்தப்படலாம்.
எடுத்துக்காட்டாக, எங்களிடம் பின்வரும் செலவு செயல்பாடு உள்ளது என்று வைத்துக்கொள்வோம்:
\(C(x) = x^3 – 6x^2 + 11x – 6\)
செலவைக் குறைக்கும் \(x\) மதிப்பைக் கண்டறிய, நியூட்டனின் முறையைப் பயன்படுத்துகிறோம். முதலில், முதல் வழித்தோன்றல் \(C'(x)\) மற்றும் இரண்டாவது வழித்தோன்றல் \(C”(x)\):
\(C'(x) = 3x^2 – 12x + 11\)
\(C”(x) = 6x – 12\)
செலவைக் குறைக்கும் \(x\) மதிப்பைத் தோராயமாக மதிப்பிடுவதற்கு மறுமுறை சூத்திரத்தைப் பயன்படுத்துகிறோம். உற்பத்திச் செலவுகளைக் குறைத்து அதிக செயல்திறனை அடையும் நோக்கத்தில் உள்ள நிறுவனங்களுக்கு இது மிகவும் பயனுள்ளதாக இருக்கும்.
லாக்ரேஞ்ச் பெருக்கி முறை
லாக்ரேஞ்ச் பெருக்கி முறை அறிமுகம்
பொருளாதாரத்தில், தேர்வுமுறை சிக்கல்கள் பெரும்பாலும் கட்டுப்பாடுகளுடன் வருகின்றன. உதாரணமாக, நுகர்வோர் பட்ஜெட் கட்டுப்பாடுகளுக்கு உட்பட்டு தங்கள் பயன்பாட்டை அதிகப்படுத்துகிறார்கள் அல்லது வரையறுக்கப்பட்ட ஆதாரங்களைக் கொண்டு நிறுவனங்கள் தங்கள் உற்பத்தியை அதிகரிக்கின்றன. லாக்ரேஞ்ச் பெருக்கி முறை என்பது ஒன்று அல்லது அதற்கு மேற்பட்ட கட்டுப்பாடுகளுக்கு உட்பட்ட ஒரு செயல்பாட்டின் லோக்கல் மாக்சிமா மற்றும் மினிமாவைக் கண்டறியப் பயன்படும் ஒரு கணித செயல்முறையாகும்.
Lagrange செயல்பாட்டின் பொதுவான வடிவம்:
\(L(x_1, x_2, \ldots, x_n, \lambda) = f(x_1, x_2, \ldots, x_n) + \lambda \cdot \left( g(x_1, x_2, \ldots, x_n) – c \ வலது)\)
இதில்:
- \(f(x_1, x_2, \ldots, x_n)\) என்பது நாம் மேம்படுத்த விரும்பும் புறநிலை செயல்பாடு ஆகும்.
- \(g(x_1, x_2, \ldots, x_n)\) என்பது கட்டுப்பாடு செயல்பாடு.
- \(\lambda\) என்பது லக்ரேஞ்ச் பெருக்கிஇது தடைக்கான புறநிலை செயல்பாட்டின் உணர்திறனைக் குறிக்கிறது.
நடைமுறை உதாரணம்: வரவு செலவுத் திட்டக் கட்டுப்பாட்டுடன் கூடிய பயன்பாட்டு அதிகரிப்பு
பட்ஜெட் கட்டுப்பாட்டுக்கு உட்பட்டு, \(x\) மற்றும் \(y\) ஆகிய இரண்டு பொருட்களை உட்கொள்வதில் இருந்து தங்கள் பயன்பாட்டை அதிகரிக்க விரும்பும் நுகர்வோரைக் கவனியுங்கள். பயன்பாட்டு செயல்பாடு பின்வருமாறு வழங்கப்படுகிறது:
\(U(x, y) = 2xy\)
நுகர்வோர் $60 பட்ஜெட்டைக் கொண்டுள்ளார், \(x\) (ஒயின்) ஒரு யூனிட்டுக்கு $5 மற்றும் \(y\) (தண்ணீர்) ஒரு யூனிட்டுக்கு $1 செலவாகும். வரவு செலவுத் தடையை இவ்வாறு வெளிப்படுத்தலாம்:
\(5x + y = 60\)
லாக்ரேஞ்ச் செயல்பாட்டை \(L(x, y, \lambda)\) பின்வருமாறு உருவாக்குகிறோம்:
\(L(x, y, \lambda) = 2xy + \lambda(60 – 5x – y)\)
உகந்த நுகர்வுத் தொகுப்பைக் கண்டறிய, \(x\), \(y\), மற்றும் \(\lambda\) உடன் \(L\) பகுதி வழித்தோன்றல்களை எடுத்து, அவற்றை பூஜ்ஜியத்திற்கு சமமாக அமைக்கிறோம்:
\\[
\frac{\partial L}{\partial x} = 2y – 5\lambda = 0
\]
\\[
\frac{\partial L}{\partial y} = 2x – \lambda = 0
\]
\\[
\frac{\partial L}{\partial \lambda} = 60 – 5x – y = 0
\]
சமன்பாடுகளின் இந்த அமைப்பைத் தீர்ப்பதன் மூலம், உகந்த நுகர்வு மூட்டையானது \(x = 6\) ஒயின் அலகுகள் மற்றும் \(y = 30\) நீர் அலகுகள் என்பதைக் காண்கிறோம். தொடர்புடைய அதிகபட்ச பயன்பாடானது \(U(6, 30) = 360\) பயன்பாட்டு அலகுகள் ஆகும்.
லாக்ரேஞ்ச் பெருக்கியின் விளக்கம்
லாக்ரேஞ்ச் பெருக்கி \(\லாம்ப்டா\) ஒரு முக்கியமான பொருளாதார விளக்கத்தைக் கொண்டுள்ளது: இது வருமானத்தின் விளிம்புப் பயன் அல்லது ஒரு யூனிட் அதிகரிப்புக்கான (எ.கா. வருமானம் அல்லது லாபம்) புறநிலை செயல்பாட்டின் மாற்றத்தைக் குறிக்கிறது (எ.கா. வருமானம் அல்லது பட்ஜெட்). எங்கள் எடுத்துக்காட்டில், \(\lambda = 12\) மதிப்பு என்பது நுகர்வோரின் பட்ஜெட் $1 ஆல் அதிகரிக்கப்பட்டால், அவற்றின் பயன்பாடு 12 அலகுகள் அதிகரிக்கும்.
நியூட்டனின் முறை மற்றும் லாக்ரேஞ்ச் முறை: எதை எப்போது பயன்படுத்துவது?
நியூட்டனின் முறை மற்றும் லாக்ரேஞ்ச் மல்டிபிளையர் முறை இரண்டும் மதிப்புமிக்க தேர்வுமுறை கருவிகள், ஆனால் அவை வெவ்வேறு நோக்கங்களுக்கு சேவை செய்கின்றன மற்றும் வெவ்வேறு சூழல்களில் பயன்படுத்தப்படுகின்றன:
நியூட்டனின் முறை கட்டுப்பாடற்ற தேர்வுமுறைக்கு மிகவும் பொருத்தமானது. மாறிகளில் வெளிப்புற வரம்புகள் இல்லாதபோது, உள்ளூர் மாக்சிமா அல்லது மினிமாவைக் கண்டறிவதற்கு இது மிகவும் திறமையானது.
லக்ரேஞ்ச் பெருக்கி முறை கட்டுப்படுத்தப்பட்ட தேர்வுமுறைக்கு ஏற்றது. பட்ஜெட், வளங்கள் அல்லது பிற வரம்புகள் போன்ற சில நிபந்தனைகளால் முடிவெடுக்கும் செயல்முறை கட்டுப்படுத்தப்படும்போது, உகந்த தீர்வுகளைக் கண்டறிய இது உதவுகிறது.
பொருளாதார பகுப்பாய்வில் பயன்பாடுகள்
செலவு குறைப்பு மற்றும் லாபத்தை அதிகப்படுத்துதல்
உகப்பாக்கம் நுட்பங்கள் செலவைக் குறைத்தல் மற்றும் லாபத்தைப் பெருக்கும் பிரச்சனைகளில் பரவலாகப் பயன்படுத்தப்படுகின்றன. நிறுவனங்கள் பெரும்பாலும் தங்கள் உற்பத்திச் செலவைக் குறைப்பதில் உள்ள சவாலை எதிர்கொள்கின்றன. நியூட்டனின் முறையைப் பயன்படுத்துவதன் மூலம், நிறுவனங்கள் செலவுகளைக் குறைக்கும் உகந்த உற்பத்தி அளவைக் கண்டறியலாம். மறுபுறம், லாக்ரேஞ்ச் பெருக்கி முறையானது பட்ஜெட் அல்லது திறன் கட்டுப்பாடுகளை மதிக்கும் போது வளங்களை எவ்வாறு திறமையாக ஒதுக்குவது என்பதை தீர்மானிக்க உதவும்.
நுகர்வோருக்கான பயன்பாட்டு மேம்படுத்தல்
நுகர்வோர் தங்கள் வரவுசெலவுத் திட்டக் கட்டுப்பாடுகளின் அடிப்படையில் மிக உயர்ந்த திருப்தி அல்லது பயன்பாட்டை அடைவதை நோக்கமாகக் கொண்டுள்ளனர். லாக்ரேஞ்ச் மல்டிபிளையர் முறையைப் பயன்படுத்துவதன் மூலம், தனிநபர்கள் தங்கள் வரவு செலவுத் திட்டத்தில் தங்கியிருக்கும் போது, அவற்றின் பயன்பாட்டை அதிகப்படுத்தும் பொருட்கள் மற்றும் சேவைகளின் உகந்த கலவையைத் தீர்மானிக்க முடியும். நுகர்வோர் தேர்வுக் கோட்பாடு மற்றும் தேவை நடத்தையைப் புரிந்துகொள்வதில் இந்தப் பயன்பாடு அடிப்படையானது.
உற்பத்தி உகப்பாக்கம்
Lagrange மல்டிபிளையர் முறையின் மற்றொரு பயன்பாடு உற்பத்தி மேம்படுத்தலில் உள்ளது. ஒரு நிறுவனம் இரண்டு பொருட்களை உற்பத்தி செய்கிறது மற்றும் மூலப்பொருட்கள் மற்றும் வேலை நேரங்களுக்கு மட்டுப்படுத்தப்பட்ட அணுகலைக் கொண்டுள்ளது என்று வைத்துக்கொள்வோம். லாக்ரேஞ்ச் முறையானது, வளங்களின் மீதான கட்டுப்பாடுகளைக் கருத்தில் கொண்டு, வெளியீட்டை அதிகப்படுத்தும் அல்லது செலவுகளைக் குறைக்கும் உள்ளீடுகளின் உகந்த கலவையைக் கண்டறிய நிறுவனத்தை அனுமதிக்கிறது.
உதாரணமாக, ஒரு நிறுவனம் அதன் வெளியீட்டை அதிகபட்சமாக அதிகரிக்க விரும்பினால் \(Q(x, y) = 4x^{0.5}y^{0.5}\) தொழிலாளர் மற்றும் மூலதனக் கட்டுப்பாடுகளுக்கு உட்பட்டு, உகந்த ஒதுக்கீட்டைத் தீர்மானிக்க Lagrange முறையைப் பயன்படுத்தலாம். அதிகபட்ச உற்பத்தியை அடைய இந்த வளங்கள்.
பொருளியலில் காட்சிப்படுத்தல் உகப்பாக்கம்
பொருளாதாரத்தில் தேர்வுமுறை நுட்பங்களின் விளைவுகளைப் புரிந்துகொள்வதில் காட்சிக் கருவிகள் பெரிதும் உதவுகின்றன. நியூட்டனின் முறையின் விஷயத்தில், செயல்பாட்டின் ஒரு வரைகலை பிரதிநிதித்துவம், x-அச்சுகளை தொடுகோடு வெட்டும் புள்ளிகளைக் காட்டுகிறது.
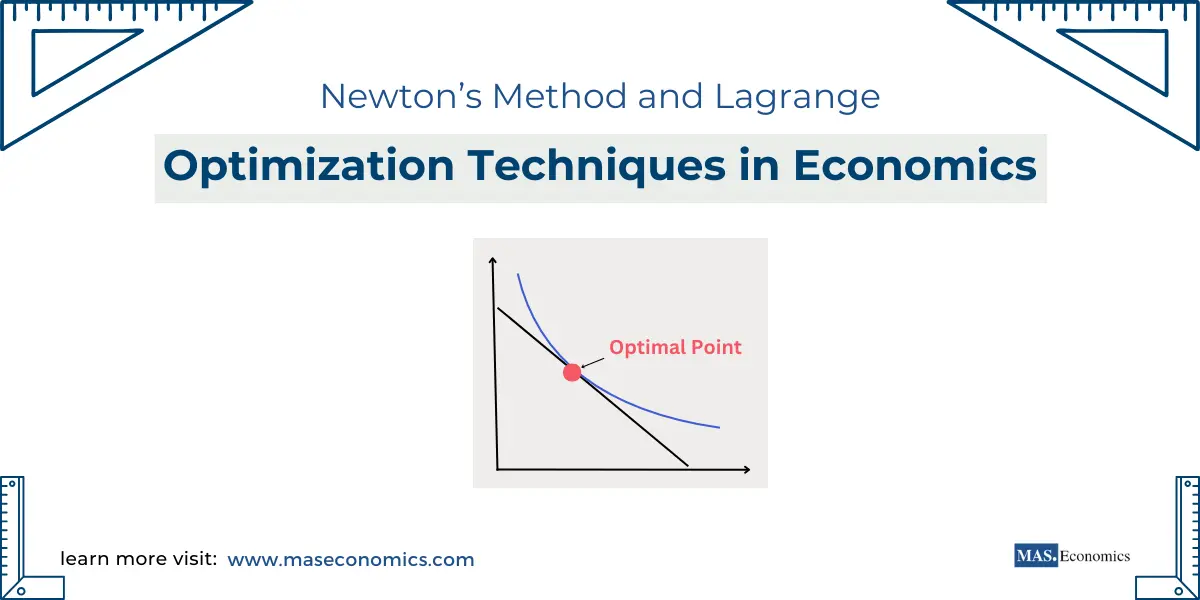
லாக்ரேஞ்ச் பெருக்கி முறைக்கு, வரைகலை பிரதிநிதித்துவங்கள் அலட்சிய வளைவுகள் மற்றும் பட்ஜெட் கட்டுப்பாடுகளை சித்தரிக்கலாம். ஒரு அலட்சிய வளைவு பட்ஜெட் கோட்டுடன் தொடும் புள்ளியானது உகந்த தீர்வைக் குறிக்கிறது, இது பட்ஜெட் கொடுக்கப்பட்ட பயன்பாட்டை அதிகப்படுத்துகிறது.
அலட்சிய வளைவுக்கும் வரவு செலவுத் திட்டத்திற்கும் இடையே உள்ள தொடர்பை விளக்கும் வரைபடம் கீழே உள்ளது. உகந்த புள்ளியாகக் குறிக்கப்பட்ட தொடுநிலை புள்ளி, கொடுக்கப்பட்ட பட்ஜெட்டின் கீழ் நுகர்வோர் பயன்பாட்டை அதிகப்படுத்தும் பொருட்களின் கலவையைக் குறிக்கிறது.
நுகர்வோர் தங்கள் வரவு செலவுத் திட்ட வரம்புகளுக்குள் அதிகபட்ச திருப்தியை அடைய தங்கள் வளங்களை எவ்வாறு திறம்பட ஒதுக்குகிறார்கள் என்பதைப் புரிந்துகொள்ள இந்த காட்சி உதவுகிறது.
முடிவுரை
நியூட்டனின் முறை மற்றும் லாக்ரேஞ்ச் மல்டிபிளையர் முறை போன்ற உகப்பாக்கம் நுட்பங்கள் பொருளாதாரத்தில் விலைமதிப்பற்ற கருவிகள் ஆகும், இது பொருளாதார வல்லுநர்கள் மற்றும் ஆய்வாளர்கள் அதிகப்படுத்துதல் மற்றும் குறைத்தல் உள்ளிட்ட சிக்கலான சிக்கல்களைத் தீர்க்க உதவுகிறது. நியூட்டனின் முறையானது கட்டுப்பாடற்ற பிரச்சனைகளுக்கு மிகவும் பயனுள்ளதாக இருக்கிறது, உகந்த உற்பத்தி நிலைகள் அல்லது செலவு குறைப்பு புள்ளிகளைக் கண்டறிய உதவுகிறது. வரவு செலவுத் திட்டங்கள் அல்லது வள வரம்புகள் போன்ற கட்டுப்பாடுகளைக் கையாளும் போது, தீர்வுகள் நிஜ-உலக வரம்புகளுக்கு மதிப்பளிக்கின்றன என்பதை உறுதிப்படுத்தும் போது, Lagrange பெருக்கி முறை இன்றியமையாதது.
அடிக்கடி கேட்கப்படும் கேள்விகள்:
நியூட்டனின் முறை என்றால் என்ன, அது பொருளாதாரத்தில் எவ்வாறு பயன்படுத்தப்படுகிறது?
நியூட்டனின் முறை என்பது ஒரு செயல்பாட்டின் வேர்களைத் தோராயமாக மதிப்பிடுவதற்குப் பயன்படுத்தப்படும் ஒரு எண்ணியல் நுட்பமாகும். பொருளாதாரத்தில், தீர்வுகளின் தோராயங்களைச் செம்மைப்படுத்துவதன் மூலம், லாப அதிகபட்சம் அல்லது செலவு குறைந்தபட்சம் போன்ற உகந்த புள்ளிகளைக் கண்டறிய உதவுகிறது. இது செயல்பாடு மற்றும் அதன் வழித்தோன்றலை தற்போதைய புள்ளியில் மதிப்பிடுவதன் மூலம் அடுத்த தோராயத்தை ஒன்றிணைக்கும் வரை கணிக்கும்.
செலவைக் குறைக்க நியூட்டனின் முறை எவ்வாறு பயன்படுத்தப்படுகிறது?
நியூட்டனின் முறையைப் பயன்படுத்தி செலவுகளைக் குறைக்க, ஒரு நிறுவனம் அதன் செலவுச் செயல்பாட்டை முதல் மற்றும் இரண்டாவது வழித்தோன்றல்களைக் கணக்கிடுவதன் மூலம் பகுப்பாய்வு செய்கிறது. எடுத்துக்காட்டாக, செலவுச் செயல்பாடு \(C(q) = q^2 – 4q + 10\) எனில், நியூட்டனின் முறையானது, செலவைக் குறைக்கும் உற்பத்தி அளவைக் கண்டறியும் வரை தீர்வைத் திரும்பத் திரும்பச் செம்மைப்படுத்துகிறது.
லாக்ரேஞ்ச் பெருக்கி முறை என்றால் என்ன, அது ஏன் முக்கியமானது?
லாக்ரேஞ்ச் மல்டிபிளையர் முறையானது கட்டுப்பாடுகள் கொண்ட தேர்வுமுறை சிக்கல்களுக்குப் பயன்படுத்தப்படுகிறது. இது ஒன்று அல்லது அதற்கு மேற்பட்ட கட்டுப்பாடுகளுக்கு உட்பட்ட ஒரு செயல்பாட்டின் அதிகபட்ச அல்லது குறைந்தபட்சத்தைக் கண்டறிய உதவுகிறது. பெருக்கி \(\lambda\) என்பது தடையில் ஒரு யூனிட் மாற்றத்துடன் (எ.கா. பட்ஜெட் அல்லது ஆதாரங்கள்) புறநிலை செயல்பாடு (எ.கா., பயன்பாடு அல்லது லாபம்) எவ்வளவு மாறுகிறது என்பதைக் குறிக்கிறது.
லாக்ரேஞ்ச் பெருக்கி முறை எவ்வாறு பயன்பாட்டை மேம்படுத்துகிறது?
பயன்பாட்டு மேம்படுத்தலில், லாக்ரேஞ்ச் முறையானது, நுகர்வோர் தங்கள் பட்ஜெட்டுக்குள் திருப்தியை அதிகரிக்க, பொருட்களின் உகந்த கலவையைக் கண்டறிய உதவுகிறது. நுகர்வோரின் பயன்பாட்டுச் செயல்பாடு \(U(x, y) = x \cdot y\) மற்றும் பட்ஜெட் கட்டுப்பாடு \(5x + y = 60\) எனில், இந்த முறை பொருட்களின் அளவு \(x\) மற்றும் \ (y\) பட்ஜெட்டை மதிக்கும் போது உபயோகத்தை அதிகப்படுத்தும்.
லாக்ரேஞ்ச் பெருக்கியின் விளக்கம் என்ன?
Lagrange பெருக்கி \(\lambda\) ஒரு யூனிட் மூலம் ஒரு தடையை தளர்த்துவதன் விளிம்பு தாக்கத்தை அளவிடும். பொருளாதார அடிப்படையில், பட்ஜெட் அல்லது உற்பத்தி செயல்முறையில் கூடுதல் டாலர் அல்லது வள அலகு சேர்க்கப்படும் போது புறநிலை செயல்பாடு (எ.கா., பயன்பாடு அல்லது லாபம்) எவ்வளவு அதிகரிக்கிறது என்பதை இது பிரதிபலிக்கிறது.
லாக்ரேஞ்ச் முறைக்குப் பதிலாக நியூட்டனின் முறை எப்போது பயன்படுத்தப்பட வேண்டும்?
பட்ஜெட் அல்லது திறன் கட்டுப்பாடுகள் இல்லாத லாபத்தை அதிகப்படுத்தும் வெளியீட்டைக் கண்டறிவது போன்ற கட்டுப்பாடற்ற தேர்வுமுறை சிக்கல்களுக்கு நியூட்டனின் முறை பொருத்தமானது. வரையறுக்கப்பட்ட பட்ஜெட்கள், வளங்கள் அல்லது உற்பத்தி திறன் போன்ற காரணிகள் தீர்வைப் பாதிக்கும் போது, கட்டுப்படுத்தப்பட்ட தேர்வுமுறைக்கு Lagrange முறை சிறந்தது.
உற்பத்தி மற்றும் செலவு பகுப்பாய்வில் இந்த தேர்வுமுறை முறைகள் எவ்வாறு பயன்படுத்தப்படுகின்றன?
நிறுவனங்கள் நியூட்டனின் முறையைப் பயன்படுத்தி செலவுகளைக் குறைக்கும் அல்லது லாபத்தை அதிகப்படுத்தும் உற்பத்தி அளவைக் கண்டறியும். இந்த வரம்புகளுக்கு மதிப்பளித்து, உழைப்பு அல்லது மூலதனம், உற்பத்தியை அதிகப்படுத்துதல் அல்லது செலவுகளைக் குறைத்தல் போன்ற உள்ளீடுகளில் நிறுவனங்கள் தடைகளை எதிர்கொள்ளும்போது, வளங்களை திறமையாக ஒதுக்குவதற்கு Lagrange முறை உதவுகிறது.
பொருளாதாரத்தில் தேர்வுமுறை ஏன் முக்கியமானது?
அதிகபட்ச வெளியீடு, லாபம் அல்லது பயன்பாட்டை அடைய தனிநபர்கள் மற்றும் நிறுவனங்கள் தங்கள் வளங்களை திறமையாக பயன்படுத்துவதை உகப்பாக்கம் உறுதி செய்கிறது. நியூட்டனின் மற்றும் லாக்ரேஞ்சின் முறைகளைப் பயன்படுத்துவதன் மூலம், பொருளாதார வல்லுநர்கள் மற்றும் முடிவெடுப்பவர்கள், வருவாயை அதிகரிக்கவும், செலவுகளைக் குறைக்கவும் மற்றும் வளங்களை திறம்பட ஒதுக்கவும் தெரிந்த தேர்வுகளை செய்யலாம்.
படித்ததற்கு நன்றி! இதை நண்பர்களுடன் பகிர்ந்து உங்களுக்கு பயனுள்ளதாக இருந்தால் அறிவைப் பரப்புங்கள்.
MASEபொருளாதாரத்துடன் மகிழ்ச்சியாக கற்றல்